📖 Value-based Deep RL
The optimal action-value function $Q^{\star}(s, a)$ can be used to control the agent: observing state $s_t$, the agent performs
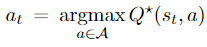
The optimal action-value function can be approximated by the neural network $Q(s, a ; \mathbf{w})$ where w captures the model parameters. The neural network is called **Deep Q Network (DQN)**.
There are different designs of network architecture. Here, we consider the game Super Mario, in which the the action space is discrete: $\mathcal{A}=\{$ "left", "right", "up" $\} .$ DQN takes state $s_t$ (which can be a screcnshot or several most recent screenshots) as input. The architecture can be
$$
\text { State } \Rightarrow \text { Conv } \Rightarrow \text { Flatten } \Rightarrow \text { Dense } \Rightarrow \text { Values. }
$$
In the Super Mario example, DQN outputs a 3-dimensional vector, e.g., [200, 100, 250], whose entries corresponds to the three actions. Then the action should be
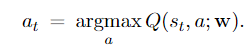
Since $Q\left(s_t\right.$, "up" $\left.; \mathrm{w}\right)=250$ is the biggest value among the three, $a_t=$ "up" will be the selected action.
DQN is typically trained using **temporal different (TD)** learning [4, 5] which allows for updating the model parameters every time a reward $R_t=r_t$ is observed. By definition, $U_t=$ $\sum_{i=1} \gamma^{i-t} \cdot R_i$. Thus
$$
U_t=R_t+\gamma \cdot U_{t+1} .
$$
TD learning makes use of the fact:
$$
Q_\pi\left(s_t, a_t\right)=\mathbb{E}\left[U_t \mid s_t, a_t\right]=\mathbb{E}\left[R_t+\gamma \cdot U_{t+1} \mid s_t, a_t\right]=\mathbb{E}\left[R_t+\gamma \cdot Q_\pi\left(S_{t+1}, A_{t+1}\right) \mid s_t, a_t\right] .
$$
Since $Q\left(s_t, a_t ; \mathbf{w}\right) \approx \max _\pi \mathbb{E}\left[U_t \mid s_t, a_t\right]$, we have
$$
Q\left(s_t, a_t ; \mathbf{w}\right) \approx r_t+\gamma \cdot Q\left(s_{t+1}, a_{t+1} ; \mathbf{w}\right) .
$$
Before observing $R_t$, the expected return was
$$
q_t=Q\left(s_t, a_t ; \mathbf{w}\right)
$$
After observing $R_t=r_t$, the expected return is updated to
$$
y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a_{t+1} ; \mathbf{w}\right)
$$
which is called **TD target**. The **TD error** is $\delta_t=q_t-y_t$. We seek to encourage a small TD error and thus define the loss:
$$
L_t=\frac{1}{2} \delta_t^2=\frac{1}{2}\left[Q\left(s_t, a_t ; \mathbf{w}\right)-y_t\right]^2 .
$$
Pretend $y_t$ is not a function of $\mathrm{w}$. Then the gradient is
$$
\left.\mathrm{g}_t \triangleq \frac{\partial L_t}{\partial \mathbf{w}}\right|_{\mathbf{w}=\mathbf{w}_t}=\left.\delta_t \cdot \frac{\partial Q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}\right|_{\mathbf{w}=\mathbf{w}_t} .
$$
The DQN can be updated by performing a gradient descent: $\mathrm{w}_{k+1} \longleftarrow \mathrm{w}_k-\alpha \cdot \mathbf{g}_t$ where $\alpha$ is the learning rate.