📖 Target Network & Double DQN
# Boostrapping 自举
$$
\text { Bootstrapping: To lift oneself up by his bootstraps. }
$$
- In $\mathrm{RL}$, bootstrapping means "using an estimated value in the update step for the same kind of estimated value".
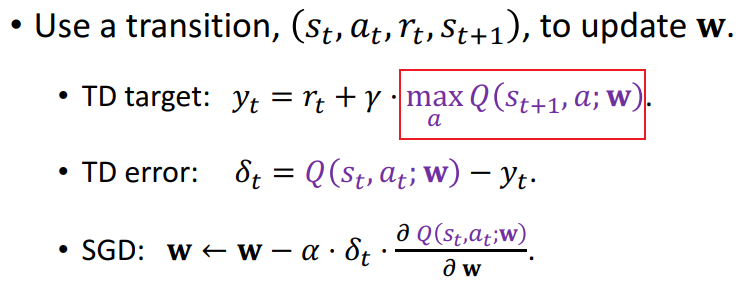
- ==TD target $y_t$ is partly an estimate made by the DQN $Q$.==
- ==We use $y_t$, which is partly based on $Q$, to update $Q$ itself.==
# Problems of Over-estimation
- TD learning makes DQN overestimate action-values. (Why?)
- <font color='red'>Reason 1: The maximization.</font>
- TD target: $y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}\right)$.
- TD target is bigger than the real action-value.
- <font color = 'red'>Reason 2: Bootstrapping propagates the overestimation.</font>
## Reason 1: Maximization

- True action-values: $x\left(a_1\right), \cdots, x\left(a_n\right)$.
- Noisy estimations made by DQN: $Q\left(s, a_1 ; \mathbf{w}\right), \cdots, Q\left(s, a_n ; \mathbf{w}\right)$.
- Suppose the estimation is unbiased:
$$
\text{mean}_a(x(a))=\text{mean}_a(Q(s, a ; \mathbf{w})) .
$$
- $q=\max _a Q(s, a ; \mathbf{w})$, is typically an overestimation:
$$
q \geq \max _a(x(a))
$$
- We conclude that $q_{t+1}=\max _a Q\left(s_{t+1}, a ; \mathbf{w}\right)$ is an overestimation of the true action-value at time $t+1$.
- The TD target, $y_t=r_t+\gamma \cdot q_{t+1}$, is thereby an overestimation.
- TD learning pushes $Q\left(s_t, a_t ; \mathbf{w}\right)$ towards $y_t$ which overestimates the true action-value.
## Reason 2:Bootstrapping
-TD learning performs bootstrapping.
-TD target in part uses $q_{t+1}=\max _a Q\left(s_{t+1}, a ; \mathbf{w}\right)$.
- Use the TD target for updating $Q\left(s_t, a_t ; \mathbf{w}\right)$.
- Suppose DQN overestimates the action-value.
- Then $Q\left(s_{t+1}, a ; \mathbf{w}\right)$ is an overestimation.
- The maximization further pushes $q_{t+1}$ up.
- When $q_{t+1}$ is used for updating $Q\left(s_t, a_t ; \mathbf{w}\right)$, the overestimation is propagated back to $\mathrm{DQN}$.
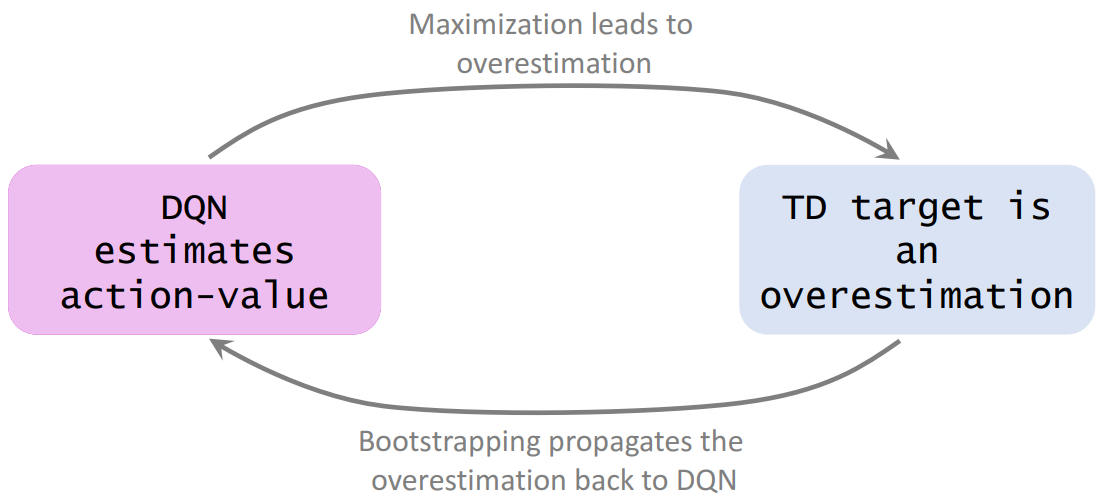
## Why is overestimation harmful?



# Solutions
- Problem: DQN trained by TD overestimates action-values.
- Solution 1: Use a target network [1] to compute TD targets. (Address the problem caused by bootstrapping.)
- Solution 2: Use double DQN [2] to alleviate the overestimation caused by maximization.
**Reference**:
1. Mnih et al. Human-level control through deep reinforcement learning. Nature, $2015 .$
2. Van Hasselt, Guez, \& Silver. Deep reinforcement learning with double Q-learning. In AAAI, 2016 .
## Target Network
- Target network: $Q\left(s, a ; \mathbf{w}^{-}\right)$
- The same network structure as the DQN, $Q(s, a ; \mathbf{w})$.
- Different parameters: $\mathbf{w}^{-} \neq \mathbf{w}$.
- Use $Q(s, a ; \mathrm{w})$ to control the agent and collect experience:
$$
\left\{\left(s_t, a_t, r_t, s_{t+1}\right)\right\} .
$$
- Use $Q\left(s, a ; \mathbf{w}^{-}\right)$to compute TD target:
$$
y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}^{-}\right) .
$$
### TD learning with Target Network
- Use a transition, $\left(s_t, a_t, r_t, s_{t+1}\right)$, to update $\mathbf{w}$
- TD target: $y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}^{-}\right)$.
- TD error: $\delta_t=Q\left(s_t, a_t ; \mathbf{w}\right)-y_t$.
- SGD: $\mathbf{w} \leftarrow \mathbf{w}-\alpha \cdot \delta_t \cdot \frac{\partial Q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}$.
### Update Target Network
- Periodically update $\mathbf{w}^{-}$.
- Option 1: $\mathbf{w}^{-} \leftarrow \mathbf{w}$.
- Option 2: $\mathbf{w}^{-} \leftarrow \tau \cdot \mathbf{w}+(1-\tau) \cdot \mathbf{w}^{-}$.
### Comparisons
- TD learning with naïve update:
TD Target: $y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}\right)$.
- TD learning with target network:
TD Target: $y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}^{-}\right)$.
- Though better than the naïve update, TD learning with target network nevertheless overestimates action-values.
## Double DQN
1. naive update
- Selection using DQN:
$$
a^{\star}=\underset{a}{\text{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}\right) .
$$
- Evaluation using DQN:
$$
y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}\right) .
$$
- Serious overestimation.
2. using target network
- Selection using target network:
$$
a^{\star}=\underset{a}{\text{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}^{-}\right) .
$$
- Evaluation using target network:
$$
y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}^{-}\right) .
$$
- It works better, but overestimation is still serious.
3. Double DQN
- Selection using DQN:
$$
a^{\star}=\underset{a}{\text{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}\right) .
$$
- Evaluation using target network:
$$
y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}^{-}\right) .
$$
- It is the best among the three; but overestimation still happens.
### Why does double $\mathrm{DQN}$ work better?
- Double DQN decouples selection from evaluation.
- Selection using DQN: $a^{\star}=\underset{a}{\text{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}\right)$.
- Evaluation using target network: $y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}^{-}\right)$.
- Double DQN alleviates overestimation:
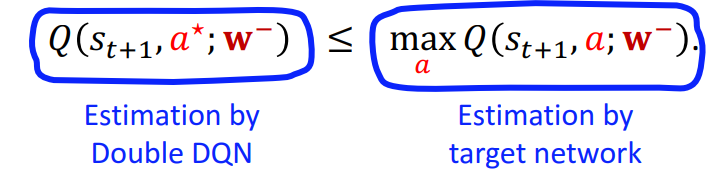
# summary

