📖 Dueling Network
# Advantage Function


**Definition: Optimal advantage function.**
$$
A^{\star}(s, a)=Q^{\star}(s, a)-V^{\star}(s)
$$
## Properties of Advantage Function
**Theorem 1**: $\quad V^{\star}(s)=\max _a Q^{\star}(s, a)$
- Recall the definition of the optimal advantage function:
$$
A^{\star}(s, a)=Q^{\star}(s, a)-V^{\star}(s) .
$$
- It follows that
$$
\begin{aligned}
\max _a A^{\star}(s, a)=\max _a Q^{\star}(s, a)-V^{\star}(s)
=& 0
\end{aligned}
$$
**Theorem 2**: $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)-\max A^{\star}(s, a)$
# Dueling Network
1. Approximating Advantage Function
- Approximate $A^{\star}(s, a)$ by a neural network, $A\left(s, a ; \mathbf{w}^A\right)$.
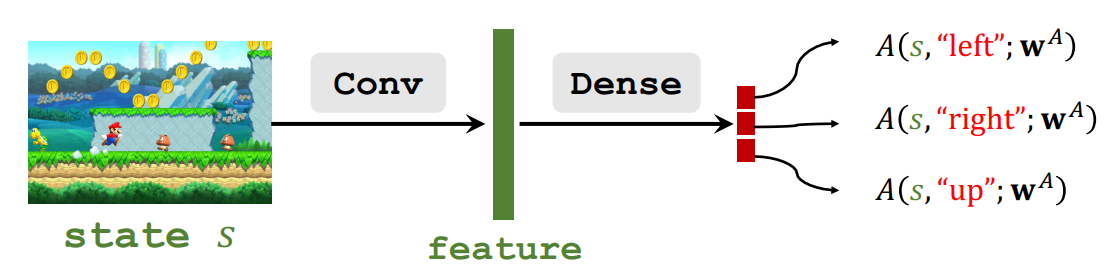
2. Approximating State-Value Function
- Approximate $V^{\star}(s)$ by a neural network, $V\left(s ; \mathbf{w}^V\right)$
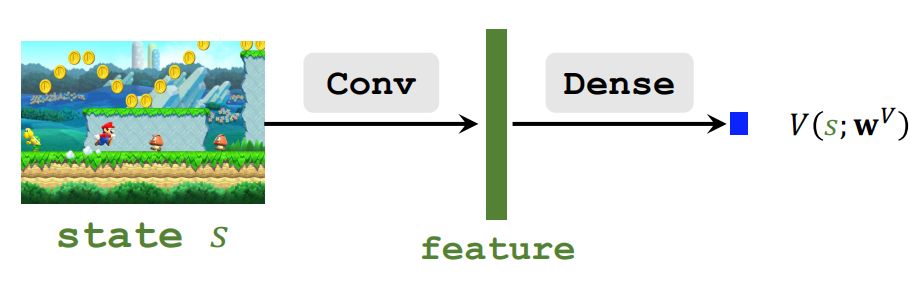
## Formulation
- Approximate $V^{\star}(s)$ by a neural network, $V\left(s ; \mathbf{w}^V\right)$.
- Approximate $A^{\star}(s, a)$ by a neural network, $A\left(s, a ; \mathbf{w}^A\right)$.
- Thus, approximate $Q^{\star}(s, a)$ by the dueling network:
$$
Q\left(s, a ; \mathbf{w}^A, \mathbf{w}^V\right)=V\left(s ; \mathbf{w}^V\right)+A\left(s, a ; \mathbf{w}^A\right)-\max _a A\left(s, a ; \mathbf{w}^A\right) .
$$
- let $\mathbf{w}=\left(\mathbf{w}^A, \mathbf{w}^V\right)$
---
$$
Q(s, a ; \mathbf{w})=V\left(s ; \mathbf{w}^V\right)+A\left(s, a ; \mathbf{w}^A\right)-\max _a A\left(s, a ; \mathbf{w}^A\right)
$$
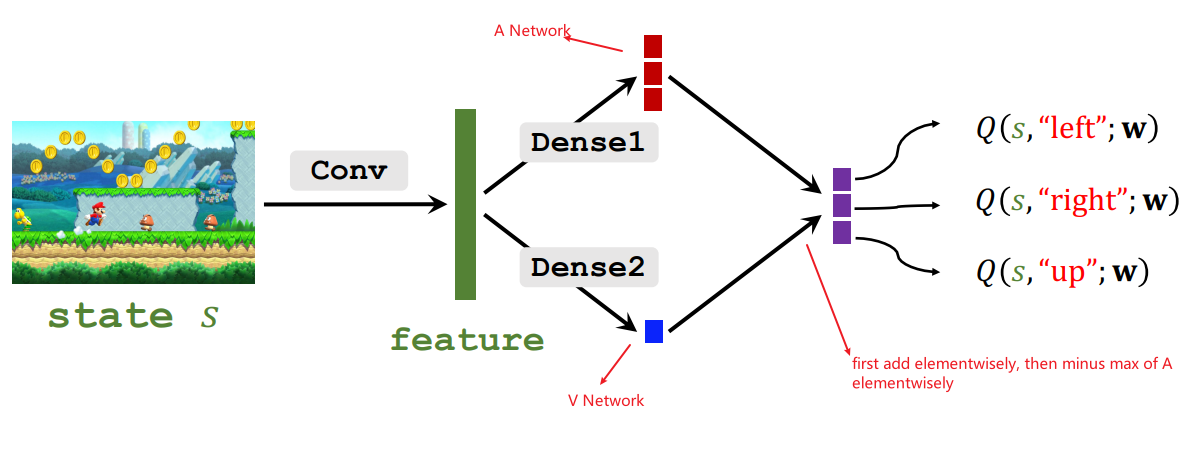
## Training
- Dueling network, $Q(s, a ; \mathbf{w})$, is an approximation to $Q^{\star}(s, a)$.
- Learn the parameter, $\mathbf{w}=\left(\mathbf{w}^A, \mathbf{w}^V\right)$, in the same way as the other DQNs.
- Tricks can be used in the same way.
- Prioritized experience replay.
- Double DQN.
- Multi-step TD target.
## Overcome non-identifiability
- Equation 1: $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)$
- Equation 2: $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)-\max _a A^{\star}(s, a)$
Question: Why is the zero term necessary?
- Equation 1 has the problem of non-identifiability.
- Let $V^{\prime}=V^{\star}+10$ and $A^{\prime}=A^{\star}-10$.
- Then $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)=V^{\prime}(s)+A^{\prime}(s, a)$.
- Why is non-identifiability a problem?
- Equation 2 does not have the problem.
## in practice

# summary
- Dueling network:
$$
Q(s, a ; \mathbf{w})=V\left(s ; \mathbf{w}^V\right)+A\left(s, a ; \mathbf{w}^A\right)-\text{mean}_a A\left(s, a ; \mathbf{w}^A\right) .
$$
- Dueling network controls the agent in the same way as DQN.
- Train dueling network by TD in the same way as DQN.
- (Do not train $V$ and $A$ separately.)