📖 Sarsa 算法
# Sarsa
- Use $\left(s_t, a_t, r_t, s_{t+1}, a_{t+1}\right)$ to update $Q_\pi$ model.
- State-Action-Reward-State-Action (SARSA).
## Sarsa (tabular version)
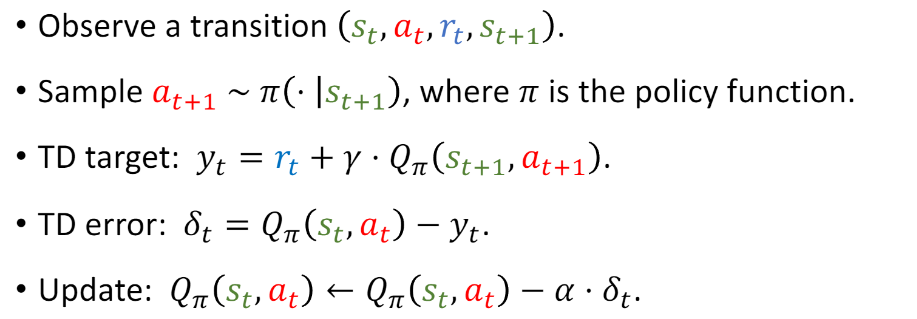
## Sarsa (Neural Network version)
model $Q_\pi(s, a)$ as a value network, $q(s, a ; \mathbf{w})$.
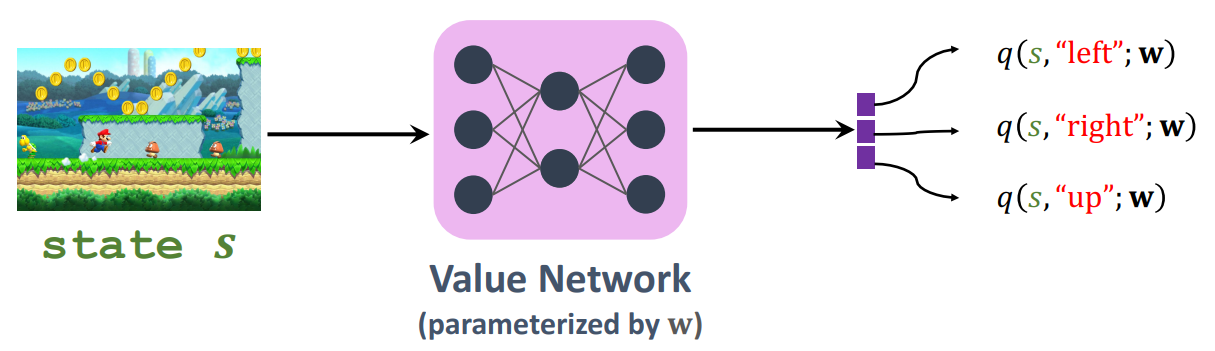
- $q$ is used as the critic who evaluates the actor. (Actor-Critic Method.)
- We want to learn the parameter, w.
### TD Error & Gradient
- TD target: $y_t=r_t+\gamma \cdot q\left(s_{t+1}, a_{t+1} ; \mathbf{w}\right)$.
- TD error: $\delta_t=q\left(s_t, a_t ; \mathbf{w}\right)-y_t$.
- Loss: $\delta_t^2 / 2$.
- Gradient: $\frac{\partial \delta_t^2 / 2}{\partial \mathbf{w}}=\delta_t \cdot \frac{\partial q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}$.
- Gradient descent: $\mathbf{w} \leftarrow \mathbf{w}-\alpha \cdot \delta_t \cdot \frac{\partial q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}$.
# Derive TD Target
The discounted return:
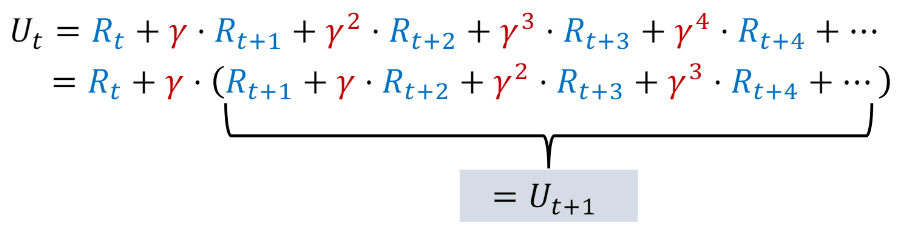
**Identity 1**: $U_t=R_t+\gamma \cdot U_{t+1}$
Assume $R_t$ depends on $\left(S_t, A_t, S_{t+1}\right)$
$$
\begin{aligned}
Q_\pi\left(s_t, a_t\right) &=\mathbb{E}\left[U_t \mid s_t, a_t\right] \\
&=\mathbb{E}\left[R_t+\gamma \cdot U_{t+1} \mid s_t, a_t\right] \\
&=\mathbb{E}\left[R_t \mid s_t, a_t\right]+\gamma \cdot \mathbb{E}\left[U_{t+1} \mid s_t, a_t\right]\\
&=\mathbb{E}\left[R_t \mid s_t, a_t\right]+\gamma \cdot \mathbb{E}\left[Q_\pi\left(s_{t+1}, A_{t+1}\right) \mid s_t, a_t\right]
\end{aligned}
$$
**Identity 2**: $\quad Q_\pi\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q_\pi\left(S_{t+1}, A_{t+1}\right)\right]$, for all $\pi$.
- We do not know the expectation.
- Approximate it using Monte Carlo (MC).
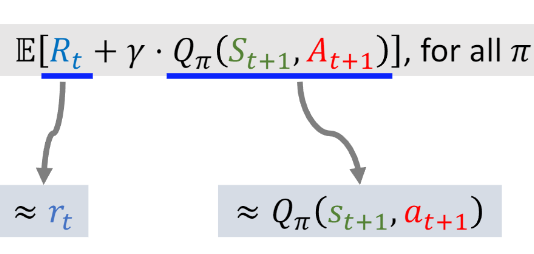
- $\approx r_t+\gamma \cdot Q_\pi\left(s_{t+1}, a_{t+1}\right)$ = TD target $y_t$
==TD learning: learn $Q_\pi\left(s_t, a_t\right)$ to approach $y_t$==
- 回归问题:
target $y_{t}$ = $r_t+\gamma \cdot Q_\pi\left(s_{t+1}, a_{t+1}\right)$
prediction $\hat{y}_{t} = Q_{\pi}(s_{t},a_{t})$
# Summary
- Goal: Learn the action-value function $Q_\pi$.
- Tabular version (directly learn $Q_\pi$ ).
- There are finite states and actions.
- Draw a table, and update the table using Sarsa.
- Value network version (function approximation).
- Approximate $Q_\pi$ by the value network $q(s, a ; \mathbf{w})$.
- Update the parameter, w, using Sarsa.
- Application: actor-critic method.